B

Thermodynamic properties of an interfacial layer

The following definitions are useful only when $V^s$ can be assessed unequivocally on the basis of a physica1 model of the interfacial layer, or when $V^s$ can be taken as negligibly small.

Interfacial energy ($U^s$) is defined by

$$U^s = U - U^{\alpha}- U^{\beta}= U - V^{\alpha}\left(\frac{U^{\al... ...}{V^{\alpha}_m}\right) -V^{\beta}\left(\frac{U^{\beta}_m}{V^{\beta}_m}\right),$$

where $U$ is the total energy of the system, and $U^{\alpha}$ and $U^{\beta}$ are the energies attributed to the bulk phases ${\alpha}$ and ${\beta}$ of volumes $V^{\alpha}$ and $V^{\beta}$ subject to the condition

$$V = V^{\alpha}+V^{\beta}+V^s,$$

where $V$ is the total volume.

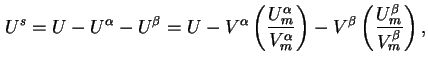
Interfacial entropy ($S^s$) is defined by

$$S^s = S - S^{\alpha}- S^{\beta}= S - V^{\alpha}\left(\frac{S^{\al... ...}{V^{\alpha}_m}\right) -V^{\beta}\left(\frac{S^{\beta}_m}{V^{\beta}_m}\right),$$

where $S$ is the total entropy of the system.

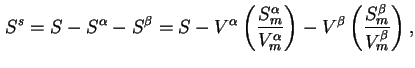
Interfacial Helmholtz energy ($A^s$) is defined by

$$A^s = U^s - TS^s.$$

The corresponding quantities per unit area may be denoted by lower case letters:

$$u^s = U^s/A_s,$$

$$s^s = S^s/A_s,$$

$$a^s = A^s/A_s.$$

Enthalpy and Gibbs energy. When the state of a system depends upon more than one pair of conjugate mechanical (or electrical) variables, i.e. more than $(p, V)$, then it is possible to derive several sets of functions having the character of enthalpies and Gibbs energies. These functions are related in the following way

Energy [r]^-xY [d]^-TS & Enthalpy[d]^-TS
Helmholtz energy [r]^-xY & Gibbs energy

where $x$ is an intensive mechanical (or electrical) variable and $Y$ the conjugate extensive variable.

The properties of interfacial layers depend on both $(p, V^s)$ and $({\gamma}, A_s)$. In defining an enthalpy in terms of the corresponding energy either $-pV^s$, ${\gamma}A_s$ or $-(pV^s -{\gamma}A_s)$ may be subtracted from the energy function. There are thus three possible definitions of interfacial enthalpy:

$$\mathscr{H}^s = U^s + pV^s,$$

$$\hat{H}^s = U^s - {\gamma}A_s,$$

$$H^s = U^s + pV^s - {\gamma}A_s,$$

and three definitions of the interfacial Gibbs energy

$$\begin{array}{rclcl} \mathscr{G}^s & = & A^s+pV^s & = &\maths... ...^s-TS^s,\\ G^s&=&A^s+pV^s-{\gamma}A_s&=&H^s-TS^s. \end{array}$$

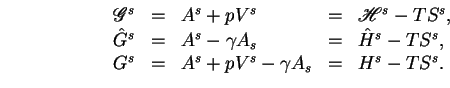
No distinguishing names have been suggested for these different functions.

A possible nomenclature, if one is needed, could be

$$\mathscr{H} = pV ,$$

$$\hat{H} = {\gamma}A ,$$

$$H = pV{\gamma}A ,$$

$$\mathscr{G} = pV ,$$

$$\hat{G} = {\gamma}A ,$$

$$G = pV{\gamma}A .$$

Of these $\hat{H}^s$ and $\hat{G}^s$ are not often used.