Surface excess energy (
![]() ) is defined by
) is defined by
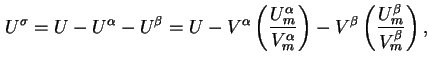
![]() and
and
![]() are the energy densities in the two bulk phases where
are the energy densities in the two bulk phases where
![]() and
and
![]() are the mean molar energies and
are the mean molar energies and
![]() and
and
![]() are the mean molar volumes of the two phases.
are the mean molar volumes of the two phases.
Surface excess entropy (
![]() ) is defined by
) is defined by
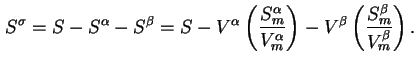
![]() and
and
![]() are the entropy densities in the two bulk phases, where
are the entropy densities in the two bulk phases, where
![]() and
and
![]() are the mean molar entropies of the two phases.
are the mean molar entropies of the two phases.
Surface excess Helmholtz energy (
![]() ) is defined by
) is defined by
Surface excess enthalpy (
![]() ) is defined by
) is defined by
Surface excess Gibbs energy (
![]() ) is defined by
) is defined by
When the thermodynamics of surfaces is discussed in terms of excess quantities,
![]() . There is thus only one way of defining the excess surface enthalpy and excess surface Gibbs energy (cf. case B, below).
. There is thus only one way of defining the excess surface enthalpy and excess surface Gibbs energy (cf. case B, below).
The corresponding excess quantities per unit area may be denoted by lower case letters:
Relative (excess) surface energy (with respect to component 1)
![$\displaystyle U^{{\sigma}(1)}=U^{\sigma}-n^{\sigma}_1\left[
\left(\frac{U^{\alp...
...\left(\frac{U^{\beta}_m}{V^{\beta}_m}\right)\right]/(c^{\alpha}_1-c^{\beta}_1).$](img198.png)
Reduced (excess) surface energy
![$\displaystyle U^{{\sigma}(n)}=U^{\sigma}-n^{\sigma}\left[
\left(\frac{U^{\alpha...
...t)
-\left(\frac{U^{\beta}_m}{V^{\beta}_m}\right)\right]/(c^{\alpha}-c^{\beta}),$](img203.png)
Analogous equations hold for
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.