|
|
Vol.
35 No. 2
March-April 2013
|
| |
Recent IUPAC technical reports and recommendations that affect the many fields of pure and applied chemistry.
See also www.iupac.org/publications/pac |
by D. Brynn Hibbert
 |
The reason for making a measurement often involves comparison of the measurement result with another result, a standard value, a legal limit, or perhaps a value written in a contract. The question addressed by the recently-published guidance document JCGM 106:2012, Evaluation of Measurement Data—The Role of Measurement Uncertainty in Conformity Assessment,1 is how to take measurement uncertainty into account when deciding whether such comparisons are satisfactory. It was fashionable at one time, particularly in legal matters, to assert that there was no uncertainty of measurement and that a prescribed limit had already taken into account any concerns of measurement error (as it was then known). This is not a good idea. Leaving aside the faulty logic, this approach does not allow changes in methods that may lead to lowering of uncertainty. With the publication of ISO/IEC 170252 evaluation of measurement uncertainty became required, and its reporting mandatory when measurement results were being assessed against limits (5.10.3.(c) “ … information on uncertainty is needed in test reports … when the uncertainty affects compliance to a specification limit;”). Thus, measurement uncertainty is now closely associated with conformity to limits, and it is not surprising that the Working Group charged with the stewardship of the GUM3 turned its attention to this important aspect of measurement uncertainty.
 |
The approach to evaluating measurement uncertainty taken by the original authors of the GUM and maintained by the JCGM-WG1 in its preparation of further guides and, at present, the second edition of the GUM itself, is that a measurement result can be expressed in terms of a probability density function (PDF), the form of which gives the value to be reported (usually the mean of the distribution) and a coverage interval in which the value of the measurand is believed to lie with a stated probability. Strategies for obtaining information about the PDF depend on the measurement problem and the data available, but the package of approaches is loosely called “Bayesian,” after the 18th century English cleric who is credited with providing the first description of the inductive probabilistic reasoning that later led Laplace to write down what is now known as Bayes Theorem.
Comparing a measurement result with a limit provides a nice example of this probabilistic approach, as one of the often-asked questions is, “what is the probability that I will make a mistake if I accept/reject this item based on my measurement result.” In the world of process control the probability of accepting an item when it should have been rejected is known as the “consumer’s risk,” and the probability of falsely rejecting the item is known as the “producer’s risk.” Each of these can be modelled in terms of the measurement result and associated measurement uncertainty, and appropriate acceptance limits can be chosen so as to balance the risks. Methods for calculation of these risks are a central focus of JCGM 106.
| Figure 1. Acceptance or rejection of an item on the basis of a measurement result. Tu is an upper tolerance limit with which a measured property must comply (the true value must be less than Tu). Au is the upper acceptance limit of the measured value. (a) shared risk (or simple acceptance) where the tolerance and acceptance limits are equal; (b) guarded acceptance, which reduces the producer's risk; (c) guarded rejection, which reduces the consumer's risk. The nomenclature follows from guidance document JCGM 106:2012. |
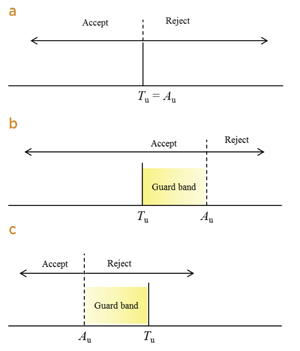 |
Simply deciding to accept a value that is within the prescribed “tolerance limit,” and to reject one that is outside shares the risk between consumer and producer. The probability of false acceptance or false rejection is equal (assuming a symmetrical PDF) for a measurement exactly at the tolerance limit. Such a “decision rule” is called simple acceptance in JCGM 106, and is often accompanied by a requirement that the expanded measurement uncertainty be no greater than a specified value.
Another decision rule described in JCGM 106 is called “guard banding.” If the consequences arising from the two errors are different, life and death in some health or forensic situations, a second limit, offset from the tolerance limit, is often prescribed (an “acceptance limit”) which defines a “guard band.” The use of a guard band reduces the probability of error for one or other of the risks and in doing so increases the probability of the other, less seriously consequential, risk. See Figure 1.
An example of guarded acceptance is found in testing race horses for administration of sodium bicarbonate, a so-called “milk shake” which raises the concentration of carbon dioxide in blood. The limit published in the rules of racing is that a horse must not be presented for racing with greater than 36 mmol L-1 “total carbon dioxide” (TCO2). TCO2 is measured by an electrochemical gas analyser with an uncertainty of about 0.2 mmol L-1. In Australia, a prosecution is not brought until the measured concentration is greater than 37 mmol L-1. The example is therefore one of Figure 1 (b) with Tu = 36 mmol L-1 and Au = 37 mmol L-1. Knowing that the standard uncertainty of the measurement is 0.2 mmol L-1 and assuming a normal distribution for the PDF of the measurement result, the odds that a sample with a measured concentration of 37 mmol L-1, causing the trainer of the horse to be liable to prosecution, actually being legal at 36 mmol L-1 or less, are about 3½ million to one against. In contrast, a horse with 37 mmol L-1 TCO2 in its blood has a one in two chance of getting away with this transgression. (For the actual uncertainty budget and calculations see reference 4).
The author thanks Dr. Tyler Estler, the principal author of JCGM 106, for his advice on this manuscript.
D. Brynn Hibbert <[email protected]> is a professor at the School of Chemistry at University of New South Wales in Sydney, Australia. He has been a member of the IUPAC Analytical Chemistry Division since 2002 and is currently the vice president.
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—The Role of Measurement Uncertainty in Conformity Assessment, JCGM 106:2012:2012 BIPM, Sèvres, www.bipm.org/utils/common/documents/jcgm/
JCGM_106_2012_E.pdf
- ISO/IEC. General Requirements for the Competence of Calibration and Testing Laboratories, 17025:1999 International Organization for Standardization, Geneva.
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, JCGM 100:2008:2008 BIPM, Sèvres, www.bipm.org/en/publications/guides/gum.html
- D.B. Hibbert, A. Stenhouse, C. Murphy, M. Jarrett, R. Osborne, J. H. Vine, L. Glowacki, C. Russo. Accred. Qual. Assur. 13 (2008).
IUPAC is one of eight organizations that comprise the Joint Committee for Guides in Metrology (JCGM), a committee of BIPM, the Bureau international des Poids et Measures: IUPAC, IUPAP, IFCC, OIML, ISO, BIPM, ILAC, and IEC. The JCGM includes two working groups: WG1 responsible for the GUM (Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement) and WG2 responsible for the VIM (International vocabulary of metrology – Basic and general concepts and associated terms); both documents are available at <www.bipm.org/en/publications/guides>. Paul De Bièvre is the IUPAC representative on the JCGM. He and René Dybkaer are the representatives on WG2, and Brynn Hibbert and René Dybkaer are IUPAC’s representatives on WG1.
IUPAC has recently endorsed and adopted the JCGM guide, Evaluation of Measurement Data—The Role of Measurement Uncertainty in Conformity Assessment (JCGM 106:2012), written by WG1. |
Page
last modified 11 March 2013.
Copyright © 2003-2013 International Union of Pure and Applied Chemistry.
Questions regarding the website, please contact [email protected] |