|
|
Vol.
33 No. 5
September-October 2011
by Ian Mills
Censullo et al. suggest the following changes to the present proposals for the new SI. They prefer explicit-unit definitions over the proposed explicit-constant definitions of all the units. They would prefer the kilogram to be redefined to fix the mass of an atom, such as the carbon 12, rather than to fix the value of the Planck constant. They would prefer the mole, and hence the Avogadro constant, to be defined to fix the molar mass of carbon 12 (which is the current definition) rather than by defining the mole explicitly by specifying the number of entities in a mole, and thus fixing the numerical value of the Avogadro constant. Each of these issues is discussed in turn below. A more detailed discussion can be found in reference 1. The copy of Resolution A for the 24th CGPM to be held in October 2011,2 and the FAQs,3 are also relevant; both are available on the BIPM website.
The distinction between explicit-unit and explicit-constant definitions may be illustrated by the present definition of the metre. The more familiar explicit-unit definition reads:
The metre is the length of path travelled by light in vacuum in 1/299 792 458 of a second.
Exactly the same definition expressed in the proposed explicit-constant form reads:
The metre, m, is the SI unit of length; its magnitude is set by fixing the numerical value of the speed of light in vacuum to be equal to exactly 299 792 458 when it is expressed in the unit m s-1.
The advantage of the explicit-constant format is that it emphasizes the reference constant used in the definition, which in this case is the speed of light, and which actually defines the unit metre per second rather than the metre. It also avoids suggesting that the definition of the metre is realized by measuring the speed of light, which is not the case. The definition of a unit should be distinguished from its realization (described as the mise en pratique for the unit), because experiments to realize a definition may change as experimental techniques develop, and new experiments may be devised. The definition of the metre, for example, is actually realized by combining sophisticated laser experiments with interferometry, which are not simple to describe, rather than by measuring the speed of light.
Explicit-constant definitions emphasize the fundamental importance of the reference constants used to define the units, rather than the base units themselves, which are less important. They also allow a simple definition of the entire system of units in a single sentence by specifying the exact numerical values of seven reference constants, as illustrated in the Resolution A proposed by the CIPM, and also in reference 1. It is important to note that the seven reference constants must be taken together to define the system. This is the most fundamental approach to defining the system of units, and it makes no reference to the base units–which indeed are not needed to define the system of units. These are the reasons why the CIPM prefer the explicit-constant format for all the definitions.
The proposed explicit-constant definition of the kilogram in the new SI reads:
The kilogram, kg, is the SI unit of mass; its magnitude is set by fixing the numerical value of the Planck constant to be equal to exactly 6.626 068 ... x10-34 when it is expressed in the unit s-1 m2 kg, which is equal to J s.
This defines the unit of action, s-1 m2 kg, rather than the unit of mass, the kg. But when taken as part of the complete set of reference constants, in which the second s is defined by fixing the caesium hyperfine frequency and the metre m by fixing the speed of light, it is seen that fixing the Planck constant h defines the kilogram.
The alternative to using h as the reference constant would be to use the mass of an atom, probably the carbon 12 atom, m(12C), or another atom, or even the mass of the electron. It is certainly true that this would have the advantage of being easier to comprehend and to teach. However choosing h has other advantages which the CIPM judge to be more important. There are two main reasons for preferring to use h as the reference constant.
The first is that in the new SI it is proposed to fix both h and e (where e is the elementary charge, the charge on a proton). This would result in exactly known values for the Josephson constant KJ = 2e/h and the von Klitzing constant RK = h/e2, which are used to interpret Josephson effect measurements of electromotive force and quantum Hall measurements of electrical resistance. These are now universally used for all precise electromagnetic measurements, and if the values of KJ and RK were exactly known it would bring all electrical measurements into the SI. The present practice is to use the conventional values KJ-90 and RK-90 that were the best estimates of these constants in 1990, in order to ensure international consistency in electrical units. But these conventional values are not consistent with the other SI units. For this reason, workers in the field of electromagnetism are strongly in favor of fixing h and e, and they are a very important community.
The second reason is that the c, h, and e are the most fundamental constants of physics, in relation to relativity, quantum mechanics, and quantum electronics respectively. It is the overall objective of the new SI to base all our units on the fundamental constants of nature, and these three constants top the list. Since we are choosing a system of units for the world that may last for many years, there are compelling reasons for choosing the most fundamental constants of physics as the reference constants to be fixed.
It is important to add that an alternative definition in terms of the mass m(12C) would be only very slightly different from the definition in terms of h, because of the fundamental relation of physics:
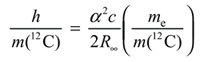 |
(1) |
That relation does not involve any units; it expresses relations between the values of the quantities involved that must be satisfied whatever units are used.1 The product of factors on the right hand side is known at present with a relative standard uncertainty of less than 1x10-9, which is more than an order of magnitude smaller than the present uncertainty in h or m(12C). Thus, h may be calculated from m(12C), and, hence, fixing h, or fixing m(12C), are almost equivalent definitions. The CIPM prefers the definition to fix h, for the reasons described above. This definition will be realized by using any experiment that at present may be used to determine h, such as either a watt-balance, or the XRCD experiment on a silicon 28 sphere to determine h from m(28Si) using equation (1) above where m(12C) is substituted both sides by m(28Si). The change to the new definition of the kilogram will not be made until the value of h determined by these experiments agree to a few parts in 108 (at present the best experimental results differ by about a part in 107).
Censullo et al. argue that these experiments involve expensive and complicated equipment; although this is clearly true, it is also true that this criticism applies to experiments to realize any of the definitions of SI units at the level required for modern quantum physics.
There are two quantities which are currently used to quantify the amount of a pure chemical sample in a manner that is proportional to the number of molecules, or entities, in the sample. The first is simply to use the quantity number of entities, denoted N, which is dimensionless, or of dimension 1. The second is to use the quantity amount of substance, n, which is regarded as a base quantity in the system of quantities and units currently adopted in chemistry. Amount of substance thus has its own unit in the SI, the mole, symbol mol. The two quantities N and n are related by the equation
where the conversion factor NA is the Avogadro constant. These statements are true regardless of how the mole is defined. The unit 1 for the quantity N does not need to be defined, because it is simply the unit of a count, which is 1.
There are two alternative ways of defining the mole to be considered. The first is to use the molar mass of carbon 12 as the reference constant, thus fixing exactly the value of the molar mass M(12C). This is the definition in the current SI; expressed in explicit-constant form it would read:
The mole, mol, is the SI unit of amount of substance of a specified elementary entity, which may be an atom, molecule, ion, electron, any other particle or a specified group of such particles; its magnitude is set by fixing the numerical value of the molar mass of carbon 12 to be equal to exactly 0.012 when it is expressed in the unit kg/mol.
The second is to use the Avogadro constant as the reference constant, thus fixing exactly the value of NA. Expressed in explicit-constant form it would read:
The mole, mol, is the SI unit of amount of substance of a specified elementary entity, which may be an atom, molecule, ion, electron, any other particle or a specified group of such particles; its magnitude is set by fixing the numerical value of the Avogadro constant to be equal to exactly 6.022 141 ... x1023 when it is expressed in the unit mol-1.
The CIPM is recommending that the second definition should be adopted. The reasons are that the first definition links the mole to the kilogram, whereas the second definition is independent of the other base units. The second definition is also regarded as simpler to comprehend, and to teach, and NA is regarded as a more fundamental constant than M(12C), which is not tied to any particular atom.
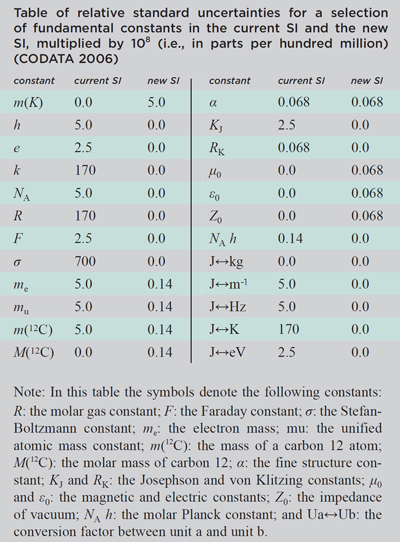
At present, M(12C) is known exactly, and NA is an experimentally determined constant with a relative standard uncertainty of 5.0x10-8 (using CODATA 2006 values of the fundamental constants). If we were to adopt the new SI recommended by the CIPM then NA would be known exactly, and M(12C) would be an experimentally determined constant; it would still have the value 12 g/mol, but it would have a relative standard uncertainty of 1.4x10-9 (see table 2 in reference 1 below). The values and experimental uncertainty in the molar masses of other atoms would remain unchanged, because the contribution from the uncertainty in the relative molar masses is significantly greater than 1.4x10-9. The actual atomic masses of the atoms are usually expressed on the atomic mass scale based on the mass of a carbon 12 atom m(12C) = 12 u exactly; none of the atomic masses expressed in either the unit u or in the kg would be changed by the new definition.
The proposals for the new SI recommended by the CIPM involve using the fundamental constants h, e, and NA as three of the reference constants that would take fixed values in the new SI. The details of the proposed changes to the definitions of the units are explained in greater detail in reference 1. The overall effect of the changes will be to reduce the uncertainty with which almost all of the fundamental constants of physics are known by more than an order of magnitude, as shown in the table of uncertainties to the right.1 In the new SI proposed by the CIPM, the unit of mass, in addition to all the other SI units, will be referenced to a true invariant of nature rather than a prototype artifact whose mass is known to be varying, perhaps by more than a part in 107 since it was adopted over a century ago.
 |
- I.M. Mills, T.J. Quinn, P.J. Mohr, B.N. Taylor and E.R. Williams, “Adapting the International System of Units to the 21st century,” Phil Trans Roy Soc 2011 (in press).
- BIPM 2011, Resolution A for the 24th meeting of the CGPM, On the Possible Future Revision of the International System of Units, the SI.
www.bipm.org/utils/common/pdf/24_CGPM_Convocation_Draft_Resolution_A.pdf
- BIPM 2011, Frequently Asked Questions about the New SI: www.bipm.org/en/si/new_si/faqs.html
Ian Mills <[email protected]> is an emeritus professor of chemistry at the University of Reading, UK, and is the current president of CCU.
Page
last modified 6 September 2011.
Copyright © 2003-2011 International Union of Pure and Applied Chemistry.
Questions regarding the website, please contact [email protected] |